Funding Areas

The Proton Spin Crisis

An experiment carried out in the 1980s has shown that quarks contribute quite a small portion to the proton spin [1]. This result is inconsistent with the present opinion of the particle physics community concerning the proton structure. This is the reason why the result of [1] is called the Proton Spin Crisis (PSC). The current (November 2019) Wikipedia PSC item states: “The problem is considered one of the important unsolved problems in physics”. This quotation indicates that a discussion of the proton structure is a timely issue.

It is argued here that general laws of quantum mechanics should provide an explanation to PSC. The Appendix contains headlines that indicate where one should look for in order to find  a resolution to the following problem:

Problem: What is a theoretically consistent explanation for the Proton Spin Crisis?

Discussion about multiconfiguration structure

Here are few points that briefly explain the multiconfiguration structure of a several particle quantum state.

1. In order to obtain an Eigen-function of the Hamiltonian, one has to diagonalize the Hamiltonian matrix.
2. The well-known laws of angular momentum coupling show how a configuration can produce an appropriate overall angular momentum.
3. For a system that comprises one kind of Dirac particles, one can construct a Hilbert space whose basis is made of Slater determinants of a configuration where the angular momentum of its single particles are coupled and produce a well-defined overall angular momentum.
4. The Hamiltonian conserves angular momentum. In cases of electromagnetic and strong interactions, the Hamiltonian also conserves parity. Hence, all Slater determinants of the Hilbert space, that are coupled with the same overall angular momentum and have the same parity, may contribute to a non-zero off-diagonal matrix element of the Hamiltonian.
5. Item D proves that a Hamiltonian whose Hilbert space is determined by configurations, is not diagonal, because some of its off-diagonal matrix elements do not vanish.
6. A diagonalization of this Hamiltonian proves that every Eigen-function of the Hamiltonian (including that of the ground state) is a linear combination of configurations.
7. The case of the proton is much more complicated, because it has two kinds of valence quarks as well as additional 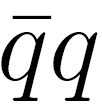pair(s). Therefore, an acceptable description of the proton state requires many configurations. This feature explains why quarks’ spin is smeared.

8. A typical error says that the members of a qq pair have identical wave-function. This is certainly wrong. Indeed, every kind of charge of members of a 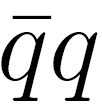pair takes an opposite sign. For this reason, they interact differently.

References

[1] A. Ashman et al., Phys. Lett. B206, 364 (1988).