Antiquarks in the Proton
The momentum distribution of the nucleon’s quarks and that of its antiquarks are
known for quite a long time (see [1], p. 281). Fig. 1 describes these data. The graphs
of fig. 1 show that the width of the distribution of quarks’ momentum is much larger than that of antiquarks. The width of the distribution is due to the Fermi motion of the proton constituents (see [1] p. 271). Using the Heisenberg uncertainty principle, one concludes that the volume of the nucleon’s quarks is much smaller than that of antiquarks.
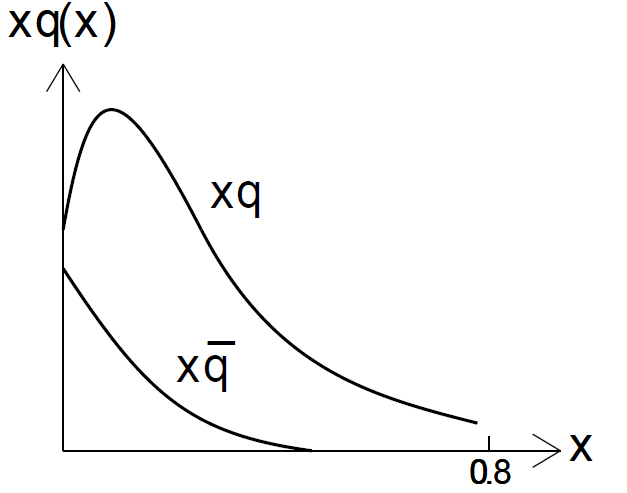
Figure 1: The graphs describe momentum distribution of quarks and antiquarks in a nucleon. (See text.)
Table 1 describe experimental data (see [2]) which illuminate the problematic
aspect of this conclusion. (R denotes the particle’s charge radius).
Table 1:
Data of particles

The data of table 1 shows that:
1. The intensity of the 2-body interaction of one ![]() pair of the
pair of the ![]() is much stronger
is much stronger
than that of the combined three ![]() pairs of the nucleon.
pairs of the nucleon.
2. The stronger ![]() bound pair of the
bound pair of the ![]() is enclosed in a smaller volume.
is enclosed in a smaller volume.
Research topic #1: Is the stronger interaction and the smaller volume of the ![]()
pair consistent with the QCD asymptotic freedom?
Research topic #2: If one quark of the pion can hold an antiquark in a volume
which is smaller than that of the proton then why the proton’s quarks do not hold
its antiquark in a volume that is not larger than that of the proton’s quarks?
Research topic #3: Why the proton contains more ![]() antiquark than
antiquark than ![]() antiquarks?
antiquarks?
(See [3] and references therein.)
References
[1] D. H. Perkins, Introduction to High Energy Physics (Addison-Wesley, Menlo Park
CA, 1987).
[2] M. Tanabashi et al. (Particle Data Group), Phys. Rev. D 98, 010001 (2018).
http://pdg.lbl.gov/2018/listings/contents_listings.html
[3] M. Alberg, Prog. Part. Nucl. Phys. 61 140 (2008).
