The EMC Effect Problem
The EMC effect was discovered more than 30 years ago [1]. The experiment measured the ratio ![]() between the
between the ![]() -distribution of quarks of the iron nucleus and the corresponding quantity of the deuteron. The data are limited to
-distribution of quarks of the iron nucleus and the corresponding quantity of the deuteron. The data are limited to ![]() <0:7. The curved lines of fig. 1 provide a description of QCD-compatible predictions of
<0:7. The curved lines of fig. 1 provide a description of QCD-compatible predictions of ![]() . It turns out that these predictions strongly disagree with the experimental data (see the decreasing line in fig. 2). Other experiments have later confirmed the EMC effect at the region of
. It turns out that these predictions strongly disagree with the experimental data (see the decreasing line in fig. 2). Other experiments have later confirmed the EMC effect at the region of ![]() <0:7 and demonstrated that the effect increases with the nucleon number A of nuclei. The new experiments also contain data of higher
<0:7 and demonstrated that the effect increases with the nucleon number A of nuclei. The new experiments also contain data of higher ![]() and show that the graph of the ratio R changes direction and turns upwards for
and show that the graph of the ratio R changes direction and turns upwards for ![]() >0:75 [2, 3, 4].
>0:75 [2, 3, 4].
This evidence does not change the general features of the experiment, because the actual number of quarks at ![]() >0:75 is negligible (see [5], p. 281, [6], p. 202).
>0:75 is negligible (see [5], p. 281, [6], p. 202).
In order to find the mean momentum of quarks, one must multiply the data represented in fig. 2 by the ![]() -population of quarks. It turns out that most quarks are found at small
-population of quarks. It turns out that most quarks are found at small ![]() (see [5], p. 281, [6], p. 202). It means that the
(see [5], p. 281, [6], p. 202). It means that the ![]() -width of quarks of heavier nuclei is smaller than that of lighter nuclei.
-width of quarks of heavier nuclei is smaller than that of lighter nuclei.
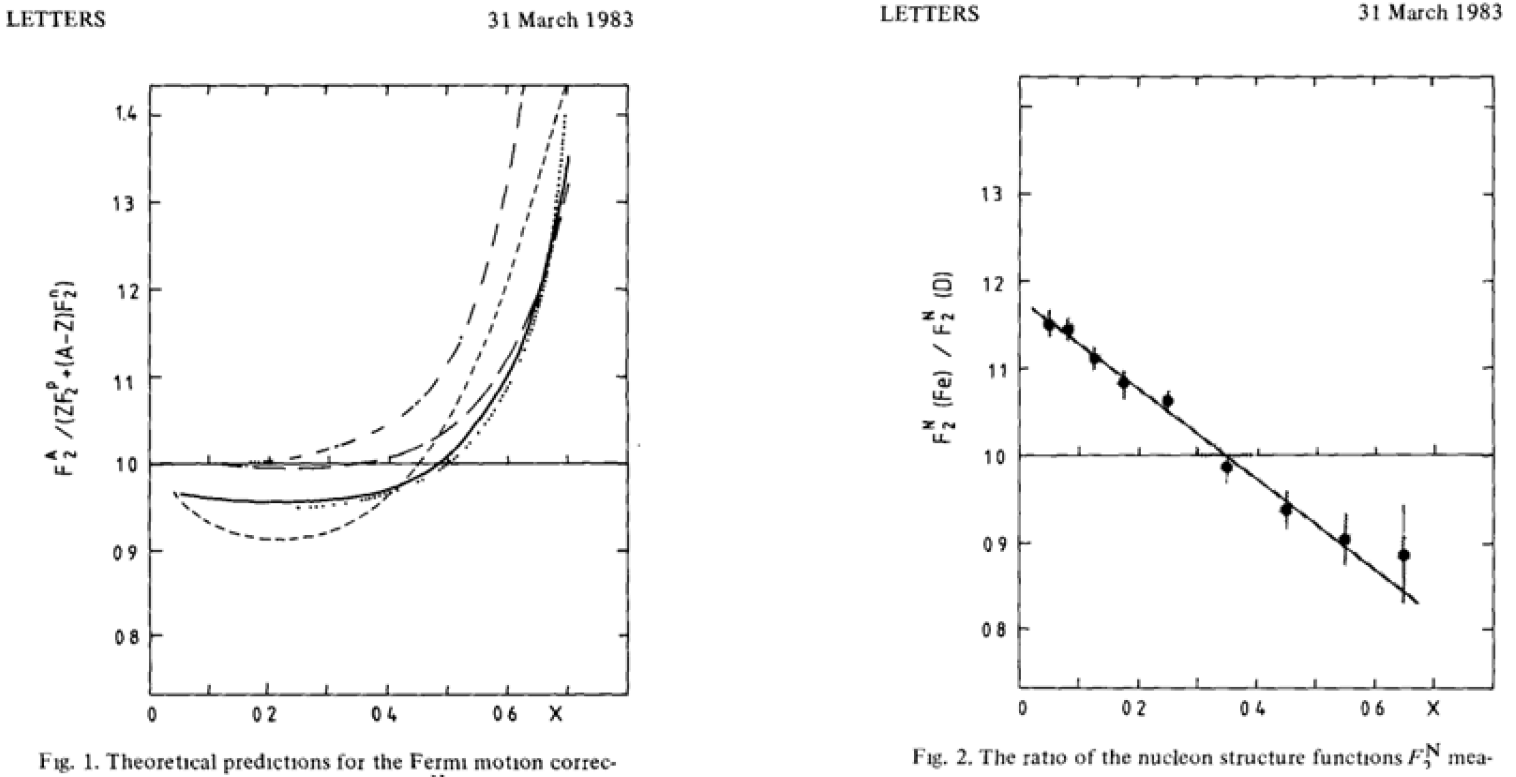
Figure 1: QCD compatible predictions [1]. Figure 2: Actual measurements [1].
The increase of the quarks’ Fermi motion increases the width of the ![]() -dependence of the graph of the scattering cross section (see [5], p. 268-269). The smaller Fermi motion of quarks of heavy nuclei and the uncertainty principle mean that the average self-volume of quarks increases with the nuclear number A.
-dependence of the graph of the scattering cross section (see [5], p. 268-269). The smaller Fermi motion of quarks of heavy nuclei and the uncertainty principle mean that the average self-volume of quarks increases with the nuclear number A.
QCD Inconsistency
As shown in the first report on the EMC effect [1], QCD, which is the prevailing strong interaction theory, has provided predictions that are inconsistent with the effect (see fig. 1 and fig. 2). Report [1] concludes: “We are not aware of any published detailed prediction presently available, which can explain the behavior of these data.” To date, this inconsistency is still a mystery, as concluded in [7] “During this time no single explanation for the effect has been forthcoming” and in [4] “So, while the experimental signature is clear, the interpretation of the effect is, at present, ambiguous.”
The Significance of the Liquid Drop Model
It turns out that a similar effect is well known in electrons. Conductors are extreme phenomenon and their electrons move freely along a macroscopic distance.
Electronic bands of solids and of liquids [8] indicate that the self-volume of electrons of a single molecule is smaller than that of electrons of the same molecules in a condense matter state. In the case of electrons, the increase of the electron’s volume in a condensed matter state is a self-evident phenomenon. Here electrons of a neighboring molecule screen the Coulomb attraction of the molecule’s nuclei and the reduced attraction yields an increase of the electron’s self-volume. Therefore, a theory that explains the nuclear liquid drop model ([9], pp. 139-141) could provide a successful interpretation to this phenomenon as well.
Research topic #1: What is a theoretically consistent explanation for the EMC effect?
Research topic #2: Is the similarity between quarks in nuclei and electrons in a liquid drop relevant to the first problem?
References
[1] J. J. Aubert et al. (EMC), Phys. Lett. 123B, 275 (1983).
[2] J. Gomez et. al., Phys. Rev. D49, 4348 (1994).
[3] O. Hen, G. A. Miller, E. Piasetzky and L. B. Weinstein, Rev. Mod. Phys. 89, 045002-1 (2017).
[4] J. Arrington, J. Phys. Conference Series, 69, 012024 (2007).
[5] D. H. Perkins, Introduction to High Energy Physics (Addison-Wesley, Menlo Park CA, 1987).
[6] M. Thomson, Modern Particle Physics (Cambridge University Press, Cambridge, 2013).
[7] P R Norton, Rep. Prog. Phys. 66, 1253 (2003).
[8] J. B. Pendry, J. Phys. C13, 3357 (1980).
[9] S. S. M. Wong, Introductory Nuclear Physics (Wiley, New York, 1998).
[10] C. F. von Weizscker, Zeit. Phys. 96, 431(1935).
[11] E. Comay, Elect. J. Theor. Phys., 9, 93-118 (2012).
http://www.ejtp.com/articles/ejtpv9i26p93.pdf
