Funding Areas

Isospin States of Mesons and Baryons

The following discussion is based on the assumed validity of QCD. Table 1 shows physical properties of four particles, each of which contains two valence quarks of the flavor [1].

Table 1: Physical Properties of Particles

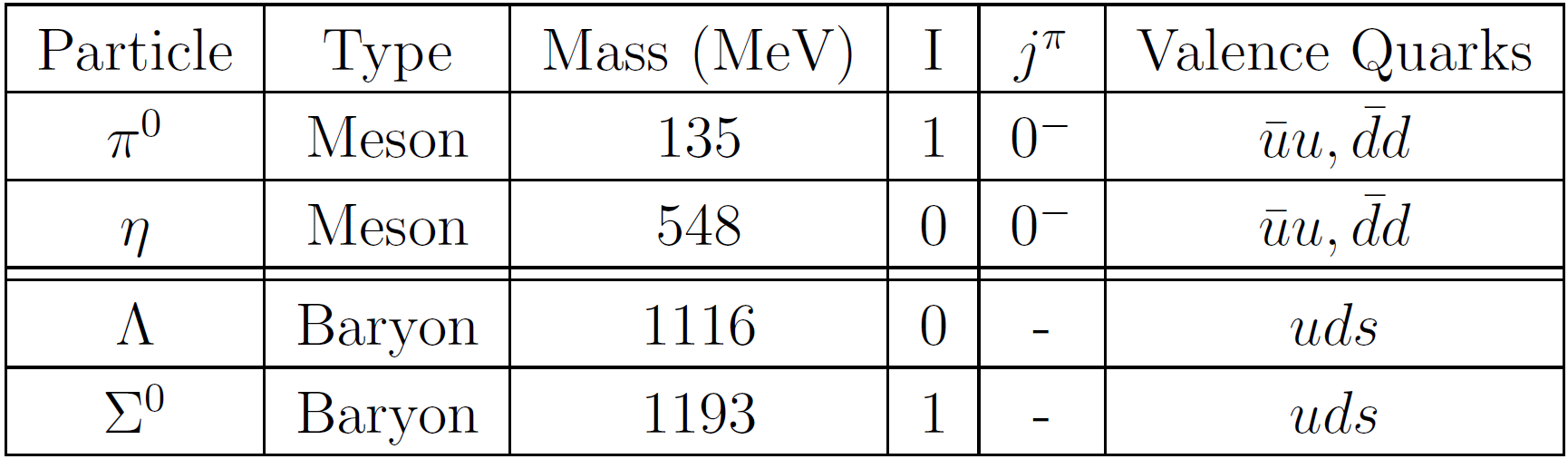
The mesons   of table 1 comprise . Therefore, every hadronic theory of these states is not affected by the Pauli Exclusion Principle, and thus these quarks may take the lowest state of kinetic energy. According to QCD, similar conclusions apply to the baryons. Here the isospin concept considers the quarks to be the same particle with different eigenvalue of the operator. Note that the Pauli Exclusion Principle allows these 2 particles to be in the lowest kinetic state. In conclusion, all quarks of table 1 are free to take the lowest state of kinetic energy.

Consider the two mesons and the two  baryons of table 1. Members of each pair comprise the same valence quarks and the different isospin symmetry indicates that for each pair, the symmetry of the state is not the same. This issue affects the mass difference between members of each pair. Table 1 shows that the isospin dependence of the mass difference between the two mesons takes the reverse order with respect to that of the corresponding baryons. In the mesons, the I=1, is the lighter member of the pair, whereas in the baryons, the I=1, is the heavier member of the pair.

This issue can be restated in the language of the representation of hadronic states. Consider the lightest meson octet (see [2], p. 156 or [3], p. 36) and the lightest baryon octet (see [2], p. 152 or [3], p. 35). Each octet has two particles at its center. The data shows that the mass order of the particles at the center of these octets takes the reverse order with respect to isospin values.

As is well established, the strong interactions that determine the main properties of hadronic states, conserved flavor, parity and isospin.

Research topic #1: Why baryonic and mesonic isospin states of a pair of the quark flavor have a reversed mass order?

Research topic #2: It is clear that the mesonic state is determined by a  force, whereas in the baryonic state it is determined by a force. Explore the idea that the data of table 1 indicates that the strong force is analogous to the electric force: the force is repulsive and the force is attractive?

References

[1] http://pdg.lbl.gov/2018/listings/contents_listings.html

[2] D. H. Perkins, Introduction to High Energy Physics (Addison-Wesley, Menlo Park CA, 1987).

[3] D. Griffiths, Introduction to Elementary Particles, 2nd edition (Wiley-VCH, Weinheim, 2008).